Capítulo 7 Álgebra lineal
7.1 Introducción
El álgebra se usa en muchas de las operaciones básicas que se realizan rutinariamente, y es la base para poder aplicar y resolver problemas más complejos que involucaran gran cantidad de datos y variables. Este capitulo hace una introducción básica a conceptos y técnicas en álgebra lineal, para familiarizar al lector y sentar una base para la comprensión de casos donde soluciones analíticas no pueden emplearse y es necesario recurrir a métodos algebráicos.
7.2 Tensores
En general cualquier arreglo de datos numéricos se considera un tensor de dimensión variable, dependiendo de la estructura de los datos.
Un tensor es una representación matemática que cuantifica la variación de la magnitud con respecto a la dirección. Numéricamente se representa como una matriz y gráficamente como un elipsoide, en el caso de 3 dimensiones (Figura 7.1).
Figura 7.1: Tensor como elipsoide. Tomado de: http://www.geosci.usyd.edu.au/users/prey/Teaching/Geol-3101/Strain/ellipse.gif
Los tensores más conocidos son:
- Escalar: Tensor de orden 0, cantidad que tiene magnitud pero no dirección. Ejemplos: densidad y temperatura.
- Vector: Tensor de orden 1, cantidad que tiene magnitud y dirección. Ejemplos: velocidad, aceleración, fuerza.
- Matriz: Tensor de orden 2 o mas, arreglo de vectores en 2 o más dimensiones, con magnitud y 2 o más direcciones. Ejemplos: esfuerzo, deformación.
7.2.1 Vectores
Los vectores son representaciones univariables de datos, ya que pueden almacenar únicamente un tipo de datos. En el sentido estricto de álgebra los datos tienen que ser del tipo numérico. Los vectores se denotan con letras minúsculas (ej: \(x\)).
La estructura y representación matemática de un vector se presenta en Ecuación (7.1), mientras que la representación gráfica se presenta en la Figura 7.2:
\[\begin{equation} x = \left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right) \tag{7.1} \end{equation}\]
donde \(n\) corresponde con la dimensión del vector.
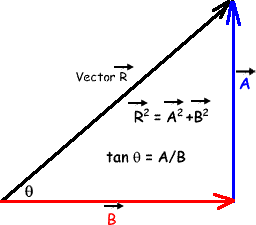
Figura 7.2: Representacion grafica de un vector. Tomado de: http://www.cyberphysics.co.uk/graphics/diagrams/forces/vector_components4.gif
7.2.1.1 Operaciones con vectores
- Suma:
\[\begin{equation} x + y = \left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right) + \left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n \end{matrix} \right) \tag{7.2} \end{equation}\]
Se requiere que ambos vectores tengan la misma dimensión. Un ejemplo seria cuando un vector contiene la concentración de \(Fe^{2+}\) y otro la de \(Fe^{3+}\), al sumarlos se obtiene la concentración total de \(Fe\) en la roca.
En R esto se realiza simplemente creando los vectores respectivos y sumandolos, porque por defecto hace la suma elemento por elemento.
Fe2 = c(2,5,4,7,10)
Fe3 = c(4,8,3,5,9)
Fe = Fe2 + Fe3
Fe## [1] 6 13 7 12 19- Multiplicación por escalar:
\[\begin{equation} \alpha x = \left( \begin{matrix} \alpha x_1\\ \alpha x_2\\ \vdots\\ \alpha x_n \end{matrix} \right) \tag{7.3} \end{equation}\]
El escalar multiplica a cada uno de los elementos. Un ejemplo seria cuando se tienen mediciones (decenas o cientos) de la longitud de fósiles en pulgadas y se desean convertir a milímetros, entonces se multiplica el vector por 25.4.
Para demostralo en R primero estoy creando un vector aleatorio de 20 datos con limite inferior de 10 y limite superior de 30. Imprimo los resultados para ver los valores, y posteriormente multiplico el vector por el escalar respectivo, de nuevo donde la operacion es elemento por elemento.
set.seed(4101)
longitud = runif(n = 20, min = 10, max = 30)
longitud## [1] 20.27580 15.18745 17.46071 15.10536 29.76256 16.82955 19.37020 22.68005
## [9] 20.54253 10.93677 12.86850 23.29475 17.20729 28.22859 13.06465 17.29120
## [17] 22.63767 20.98795 25.27941 23.9046025.4 * longitud## [1] 515.0054 385.7612 443.5020 383.6761 755.9691 427.4706 492.0031 576.0732
## [9] 521.7804 277.7939 326.8600 591.6867 437.0653 717.0062 331.8420 439.1964
## [17] 574.9968 533.0940 642.0970 607.1768- Producto punto:
\[\begin{equation} x y = \left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right) \left( \begin{matrix} y_1 & y_2 & \dotsb & y_n \end{matrix} \right) = x_1 y_1 + x_2 y_2 + \dotsb + x_n y_n \tag{7.4} \end{equation}\]
Se requiere que ambos vectores tengan la misma dimensión. Un ejemplo seria cuando el precio de los diferentes agregados (piedra de construcción) se encuentra en un vector y la cantidad del tipo de agregado se tiene en otro vector; el precio a ganar al vender dicha cantidad de acuerdo al precio establecido es el resultado del producto punto.
En R la forma de calcular el producto punto es haciendo uso del multiplicador matricial %*%, lo que arroja un resultado de una matriz de \(1 \times 1\). Lo anterior es lo mismo a hacer la suma del producto entre los vectores. Estos procedimientos se muestran a continuación.
precio = c(500, 700, 1200, 400)
cantidad = c(30, 15, 12, 23)
precio %*% cantidad## [,1]
## [1,] 49100sum(precio * cantidad)## [1] 491007.2.2 Matrices
Una matriz es una representación bivariable (2 columnas) o multivariable (> 2 columnas) de datos. Similar a los vectores, en el sentido estricto de álgebra los datos tienen que ser del tipo numérico. Las matrices se denotan con letras mayúsculas (ej: \(A\)).
La estructura y representación matemática de una matriz se presenta en Ecuación (7.5)
\[\begin{equation} A = \left( \begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{matrix} \right) \tag{7.5} \end{equation}\]
La dimensión de una matriz es el numero de filas (por lo general denominado \(i\)) por el numero de columnas (por lo general denominado \(j\)), por lo que en el caso de la matriz mostrada en (7.5) la dimensión es 9 (\(i \times j\)).
Los subíndices denotan la ubicación del elemento, siendo el primer subíndice la fila y el segundo la columna; el elemento \(a_{23}\) corresponde al elemento en la fila 2 y columna 3.
7.2.2.1 Operaciones con matrices
- Suma:
\[\begin{equation} A + B = \left( \begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{matrix} \right) + \left( \begin{matrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{matrix} \right) \tag{7.6} \end{equation}\]
Se requiere que ambas matrices tengan no solo la misma dimensión, pero la misma cantidad de filas y columnas. En este caso la operación es elemento por elemento \(a_{11} + b_{11}\). Un ejemplo seria donde una matriz contiene la producción de diversos tipos arcilla para un año dado y la otra tiene la producción para el año siguiente, la matriz resultante tiene la producción sobre esos dos años
En R simplemente se hace la suma (o resta) de las matrices, ya que hace la operación elemento por elmento.
A1 = matrix(data = c(105,218,220,63,80,76,5,2,1), nrow = 3)
A2 = matrix(data = c(84,240,302,102,121,28,4,1,0), nrow = 3)
A1 + A2## [,1] [,2] [,3]
## [1,] 189 165 9
## [2,] 458 201 3
## [3,] 522 104 1- Multiplicación por escalar:
\[\begin{equation} \alpha A = \left( \begin{matrix} \alpha a_{11} & \alpha a_{12} & \alpha a_{13}\\ \alpha a_{21} & \alpha a_{22} & \alpha a_{23}\\ \alpha a_{31} & \alpha a_{32} & \alpha a_{33} \end{matrix} \right) \tag{7.7} \end{equation}\]
El escalar multiplica a cada uno de los elementos. Un ejemplo seria cuando se tienen mediciones de los ejes de cantos de piedra en pulgadas para diversos especímenes y se requiere tenerlos en milímetros, como se muestra en el siguiente ejemplo.
cantos = matrix(data = c(3.4,4.6,5.4,2.2,4.3,4.7,1.8,4.3,4.7), nrow = 3)
25.4 * cantos## [,1] [,2] [,3]
## [1,] 86.36 55.88 45.72
## [2,] 116.84 109.22 109.22
## [3,] 137.16 119.38 119.38- Multiplicación:
\[\begin{equation} A B = \left( \begin{matrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{matrix} \right) \left( \begin{matrix} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{matrix} \right) \tag{7.8} \end{equation}\]
Se requiere que la matriz izquierda tenga la misma cantidad de columnas que filas de la matriz derecha, resultando en una matriz con dimensiones de las filas de la izquierda por las columnas de la derecha (\(A(i,j)B(m,n)=C(i,n)\)).
Se demuestra con un ejemplo trivial, pero retomando el operador de multipliación matricial %*% presentado anteriormente. Si se utiliza solo * el resultado es elemento por elemento y las matrices debieran ser de exactamente el mismo tamaño.
A1 = matrix(data = 1:9, nrow = 3)
A2 = matrix(data = 1:9, nrow = 3, byrow = T)
A1 %*% A2## [,1] [,2] [,3]
## [1,] 66 78 90
## [2,] 78 93 108
## [3,] 90 108 126- Determinante:
\[\begin{equation} A = \left( \begin{matrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{matrix} \right)\\ det(A) = |A| = a_{11} a_{22} - a_{21} a_{12} \tag{7.9} \end{equation}\]
Esto aplica para matrices cuadradas, o sea que tienen la misma cantidad de filas y columnas (\(i \times i\)). Aquí se presenta la forma manual para una matriz de \(2 \times 2\) ya que es la más sencilla, para matrices de mayor dimensión se puede hacer uso del software R, como se realiza en el siguiente ejemplo. El comando para calcular el determinante es det().
A = matrix(data = c(4,10,10,30), nrow = 2)
det(A)## [1] 207.2.2.2 Tipos de matrices
Hay ciertos tipos de matrices que de acuerdo a su estructura reciben nombres especiales. Dentro de estas matrices están:
- Diagonal: Hay entradas diferentes de cero en la diagonal y el resto de los elementos son ceros. la diagonal es donde el numero de fila y columna es el mismo (ej: \(a_{22}\)).
\[\begin{equation} \left( \begin{matrix} 3 & 0 & 0\\ 0 & 4 & 0\\ 0 & 0 & 2 \end{matrix} \right) \tag{7.10} \end{equation}\]
- Identidad: Es una matriz diagonal donde la diagonal tiene únicamente unos, y tiene una denominación especial \(I\).
\[\begin{equation} I = \left( \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{matrix} \right) \tag{7.11} \end{equation}\]
- Transpuesta: Se “rota” la matriz y lo que antes eran las filas ahora son las columnas y viceversa. Se denota por medio de \(A^T\). Si las dimensiones originales eran \((i,j)\), las dimensiones de la transpuesta son \((j,i)\).
\[\begin{equation} A = \left( \begin{matrix} 3 & 4 & 1\\ 2 & 7 & 5 \end{matrix} \right)\\ A^T = \left( \begin{matrix} 3 & 2\\ 4 & 7\\ 1 & 5 \end{matrix} \right) \tag{7.12} \end{equation}\]
- Simétrica: Se puede pensar como un espejo en los elementos no de la diagonal, donde se pueden intercambiar los subíndices y la matriz no cambia (\(a_{21} = a_{12}\))
\[\begin{equation} \left( \begin{matrix} 2 & 5 & 3\\ 5 & 1 & 4\\ 3 & 4 & 9 \end{matrix} \right) \tag{7.13} \end{equation}\]
Un caso típico de una matriz simétrica es el tensor de esfuerzos, presentado gráficamente en la Figura 7.3 y en la Ecuación (7.14).
Figura 7.3: Tensor de esfuerzos, un ejemplo de una matriz simetrica. Tomado de: https://www.efunda.com/formulae/solid_mechanics/mat_mechanics/images/StressState3D.gif
\[\begin{equation} \sigma = \left( \begin{matrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zx} & \sigma_{zz} \end{matrix} \right) \tag{7.14} \end{equation}\]
- Inversa: Cuando se multiplica la matriz original por la inversa se obtiene la matriz identidad \(I\). Se denota por medio de \(A^{-1}\). Aquí no se pretende demostrar o indicar como obtener la matriz inversa, esta se puede calcular con software dedicado para ello.
\[\begin{equation} A A^{-1} = I \tag{7.15} \end{equation}\]
7.2.2.3 Usos
Las matrices son usadas de forma rutinaria aun cuando uno no se de cuenta. Muchas de las operaciones que se realizan se pueden presentar en notación matricial, y de hecho así es como se procesan los datos a lo interno de muchas funciones. Aquí se presentan dos usos típicos y conocidos: resolver sistemas de ecuaciones y obtener predicciones para un modelo lineal.
- Sistemas de ecuaciones
Se puede resolver de dos maneras: haciendo uso de la matriz inversa (Ecuación (7.16)) o de la Regla de Cramer usando determinantes (Ecuación (7.18)).
Haciendo uso de la matriz inversa seria de la siguiente manera:
\[\begin{align*} A x &= b\\ A A^{-1} x &= A^{-1} b\\ x &= A^{-1} b \tag{7.16} \end{align*}\]
Se muestra en el siguiente ejemplo, donde se hace uso de operaciones anteriormente demostradas, primero de forma manual y seguido en R. La idea es descomponer el sistema de ecuaciones en matrices y vectores, una matriz para los coeficientes de las incógnitas, un vector para las incógnitas, y un vector para la solución de la ecuación. A partir de esto se encuentra la matriz inversa de los coeficientes, se multiplica a ambos lados de la ecuación (recordando que al multiplicar \(A A^{-1} = I\)), lo que despeja a las incógnitas y se termina de resolver el problema.
\[\begin{align*} 4 x_1 + 10 x_2 &= 38\\ 10 x_1 + 30 x_2 &= 110\\ A x &= b\\ \left( \begin{matrix} 4 & 10\\ 10 & 30 \end{matrix} \right) \left( \begin{matrix} x_1\\ x_2 \end{matrix} \right) &= \left( \begin{matrix} 38\\ 110 \end{matrix} \right)\\ A^{-1} b &= x\\ \left( \begin{matrix} 1.5 & -0.5\\ -0.5 & 2 \end{matrix} \right) \left( \begin{matrix} 38\\ 110 \end{matrix} \right) &= \left( \begin{matrix} 2\\ 3 \end{matrix} \right) \tag{7.17} \end{align*}\]
En R la inversa de una matriz se obtiene por medio de solve().
A = matrix(data = c(4,10,10,30), nrow = 2)
b = c(38,110)
Ainv = solve(A)
Ainv## [,1] [,2]
## [1,] 1.5 -0.5
## [2,] -0.5 0.2Ainv %*% b## [,1]
## [1,] 2
## [2,] 3Haciendo uso de la Regla de Cramer se muestra en el siguiente ejemplo. La idea es primero calcular el determinante de la matriz de coeficientes. Posteriormente se reemplaza la primer columna por el vector de las soluciones en la matriz de coeficientes, se calcula el determinante de esta nueva matriz y la primer incógnita (\(x_1\)) seria la división entre el determinante de la matriz modificada sobre el determinante de la matriz original. Se prosigue de manera similar para el resto de incógnitas.
\[\begin{equation} \left| \begin{matrix} 4 & 10\\ 10 & 30 \end{matrix} \right| = 4 \times 30 - 10 \times 10 = 20\\ \left| \begin{matrix} 30 & 110\\ 10 & 30 \end{matrix} \right| = 38 \times 30 - 110 \times 10 = 40\\ x_1 = \frac{40}{20} = 2\\ \left| \begin{matrix} 4 & 10\\ 30 & 110 \end{matrix} \right| = 4 \times 110 - 10 \times 38 = 60\\ x_2 = \frac{60}{20} = 3\\ \tag{7.18} \end{equation}\]
- Obtener predicciones para un modelo lineal
El procedimiento se demuestra en la Ecuación (7.19), para una regresión lineal simple (\(y = b_0 + b_1 x\)). Aquí la idea es que los valores a predecir no se toman como un vector o serie de vectores, sino que se ordenan en una matriz, donde se incluye una columna de unos para el intercepto (\(A\)). Se cuenta con un vector de los coeficientes de la regresión lineal (\(b\)). Para obtener las predicciones se realiza una multiplicación entre estas dos matrices, resultando en un vector de las predicciones deseadas (\(y\)).
\[\begin{equation} A = \left( \begin{matrix} 1 & 3.24\\ 1 & 1.37\\ 1 & 4.52\\ 1 & 4.63\\ 1 & 4.21 \end{matrix} \right); b = \left( \begin{matrix} 0.5\\ 8.1 \end{matrix} \right)\\ y = b_0 + b_1 x\\ y = A b = \left( \begin{matrix} 1 & 3.24\\ 1 & 1.37\\ 1 & 4.52\\ 1 & 4.63\\ 1 & 4.21 \end{matrix} \right) \left( \begin{matrix} 0.5\\ 8.1 \end{matrix} \right) = \left( \begin{matrix} 26.74\\ 11.59\\ 37.08\\ 38.03\\ 34.56 \end{matrix} \right)\\ \text{donde } y_1 = 0.5 \cdot 1 + 8.1 \cdot 3.24 = 26.74 \tag{7.19} \end{equation}\]
En R se hace uso de las operaciones matriciales convencionales.
A = matrix(data = c(rep(1,5), 3.24, 1.37, 4.52, 4.63, 4.21), ncol = 2)
A## [,1] [,2]
## [1,] 1 3.24
## [2,] 1 1.37
## [3,] 1 4.52
## [4,] 1 4.63
## [5,] 1 4.21a = c(0.5,8.1)
a## [1] 0.5 8.1y = A %*% a
y## [,1]
## [1,] 26.744
## [2,] 11.597
## [3,] 37.112
## [4,] 38.003
## [5,] 34.6017.3 Eigenvectors y Eigenvalues
7.3.1 Definición
Los eigenvectors (vectores característicos) son vectores especiales para una dada matriz, que al ser multiplicados por esta matriz no cambian de dirección, lo cual si ocurre con vectores no característicos. Al multiplicar la matriz por el eigenvector se obtiene un vector, el cual va a ser simplemente el eigenvector escalado (dimensionado) de acuerdo al eigenvalue (valor característico), ver Ecuación (7.20). El eigenvalue (\(\lambda\)) indica si el eigenvector es estirado (\(>1\)), comprimido (\(<1\)), invertido (valor negativo), o dejado sin cambios (\(1\)).
\[\begin{equation} A x = \lambda x \tag{7.20} \end{equation}\]
donde \(x\) es el eigenvector de \(A\) y \(\lambda\) es el eigenvalue de \(A\) para un eigenvector dado.
7.3.2 Cálculo
Primero y los más fácil es encontrar los eigenvalues, para esto se sigue el procedimiento mostrado en la Ecuación (7.21), donde la idea es despejar pasar todo a un lado de la ecuación igualando a cero, factorizar el eigenvector \(x\) y multiplicar la matriz identidad por los eigenvalues. Posteriormente a la parte factorizada se le calcula el determinante y se iguala a cero para resolver la ecuación (cuadrática en el caso de una matriz de \(2 \times 2\)) y encontrar los eigenvalues.
\[\begin{equation} \left( A - \lambda I \right) x = 0\\ \left| A - \lambda I \right| = 0 \tag{7.21} \end{equation}\]
Se puede mostrar con el siguiente ejemplo.
\[\begin{equation} A = \left( \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right)\\ \left( A - \lambda I \right) = \left( \begin{matrix} 17-\lambda & -6\\ 45 & -16-\lambda \end{matrix} \right)\\ \left| \begin{matrix} 17-\lambda & -6\\ 45 & -16-\lambda \end{matrix} \right| = 0\\ (17-\lambda)(-16-\lambda) - (45)(-6) = 0\\ \lambda^2 - \lambda - 2 = 0\\ (\lambda - 2)(\lambda + 1) = 0\\ \lambda_1 = 2, \lambda_2 = -1 \tag{7.22} \end{equation}\]
Una vez encontrados los eigenvalues se puede corroborar que cumplan con dos criterios:
- El producto de los eigenvalues es igual al determinante de la matriz original
- La suma de los eigenvalues es igual a la suma de la diagonal de la matriz original
En el caso del ejemplo mostrado en (7.22):
\[\begin{equation} \left| \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right| = (17)(-16) - (45)(-6) = -2\\ \lambda_1 = 2, \lambda_2 = -1\\ \lambda_1 \times \lambda_2 = -2 \to determinante = -2\\ \lambda_1 + \lambda_2 = 1 \to 17 - 16 = 1 \tag{7.23} \end{equation}\]
Aquí se va a obviar el procedimiento manual del cálculo de los eigenvectors, pero e muestra el resultado de los eigenvectors del ejemplo mostrado en (7.22).
Para \(\lambda_1\):
\[\begin{equation} A x = \lambda x\\ \left( \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right) \left( \begin{matrix} 2\\ 5 \end{matrix} \right) = \left( \begin{matrix} 4\\ 10\\ \end{matrix} \right)\\ \left( \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right) \left( \begin{matrix} 2\\ 5 \end{matrix} \right) = 2 \left( \begin{matrix} 2\\ 5\\ \end{matrix} \right) \tag{7.24} \end{equation}\]
Para \(\lambda_2\):
\[\begin{equation} A x = \lambda x\\ \left( \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right) \left( \begin{matrix} 1\\ 3 \end{matrix} \right) = \left( \begin{matrix} -1\\ -3\\ \end{matrix} \right)\\ \left( \begin{matrix} 17 & -6\\ 45 & -16 \end{matrix} \right) \left( \begin{matrix} 1\\ 3 \end{matrix} \right) = -1 \left( \begin{matrix} 1\\ 3\\ \end{matrix} \right) \tag{7.25} \end{equation}\]
En el siguiente ejemplo se muestra como obtener en R tanto los eigenvectors como eigenvalues, lo que se realiza mediante la función eigen().
A = matrix(data = c(17,45,-6,-16), nrow = 2)
eigen(A)## eigen() decomposition
## $values
## [1] 2 -1
##
## $vectors
## [,1] [,2]
## [1,] 0.3713907 0.3162278
## [2,] 0.9284767 0.9486833Como se menciona en los términos generales a continuación, y se ve comparando el resultado de (7.24) y (7.25) con el resultado de R, los valores de los elementos de los eigenvectors no son de importancia, sino la relación entre esos elementos. En (7.24) se muestra que el eigenvector es \(x_1=(2,5)\), pero en el ejemplo anterior es \(x_1=(0.371,0.928)\); si se hace la relación del segundo elemento por el primer elemento se obtiene \(2.5\) en ambos casos, lo mismo pasa para \(x_2\) donde la relación es de \(3\).
En términos generales:
- Los eigenvectors apuntan en la dirección que se esparcen los datos, y lo que importa es la relación entre los elementos del vector, no sus magnitudes.
- Los eigenvalues es cuaánto se esparcen los datos.
- En matrices simétricas los eigenvectors van a ser ortogonales.