Capítulo 12 Distribuciones de Probabilidad
12.1 Introducción
En el capítulo anterior se introdujeron los principios de probabilidad y las variables aleatorias (discretas y continuas), y se mencionaron las funciones (distribuciones) de probabilidad, así como unos ejemplo básicos de lo que representan. Estas distribuciones permiten aproximar de forma analítica los fenómenos que dan orígenes a las variables de interés, permitiendo obtener probabilidades para todos los posibles resultados. En este capítulo se van a introducir las distribuciones de probabilidad más utilizadas para variables discretas y continuas (haciendo referencia a una población), y que serán ampliadas en capítulos posteriores tomando en cuenta una muestra.
12.2 Distribución Binomial
Esta distribución aplica para variables discretas, de ensayos repetidos cuyo resultado se puede clasificar como de éxito (existe, está presente, está por encima, etc.) o fracaso (no existe, no está presenta, está por debajo, etc.), y la probabilidad de éxito se conoce y mantiene constante para cada ensayo (repetición) (Trauth, 2015; Triola, 2004; Walpole et al., 2012).
La Ecuación (12.1) muestra cómo se pueden obtener probabilidades para esta distribución, donde se tiene una variable \(X\) distribuida de forma binomial con \(n\) cantidad de intentos (ensayos), una probabilidad de éxito \(p\) y probabilidad de fracaso \(1-p\) para cada ensayo, y \(x \ (0,1,2,\cdots,n)\) representa el número de éxitos para el cual obtener la probabilidad.
\[\begin{equation} X \sim Bin(n,p) = \frac{n!}{(n-x)!x!} p^x q^{n-x} \tag{12.1} \end{equation}\]
Para demostrar y visualizar esta distribución se presenta el siguiente ejemplo, modificado de Trauth (2015). En el caso de una perforación para petróleo, la probabilidad de éxito está dada por 0.1 (10%). ¿Cuál es la probabilidad de tener 1 pozo exitoso de un total de 6 intentos? ¿Cuál es la probabilidad de tener al menos 2 pozos exitosos?
Lo que se tiene: \(p=0.1\), \(n=6\), y se pide la probabilidad de \(x=1\) pozo exitoso y la probabilidad de al menos 2 pozos exitosos, que es lo mismo que decir 2 o más. Una representación de la función (distribución) de densidad para este caso se muestra en la Figura 12.1. De manera manual se puede resolver de la siguiente manera.
\[\begin{align} Bin(n,p) &= \frac{n!}{(n-x)!x!} p^x q^{n-x}\\ Bin(6,0.1) &= \frac{6!}{(6-1)!1!} 0.1^1 0.9^{6-1} = 0.35 = 35 \% \end{align}\]
En R se puede usar dbinom para obtener la probabilidad puntual y pbinom para obtener la probabilidad acumulada.
p = 0.1
n = 6
x = 1
dbinom(x = x, size = n, prob = p) # probabilidad de x = 1## [1] 0.354294pbinom(q = 1, size = n, prob = p, lower.tail = F) # probabilidad de x >= 2## [1] 0.114265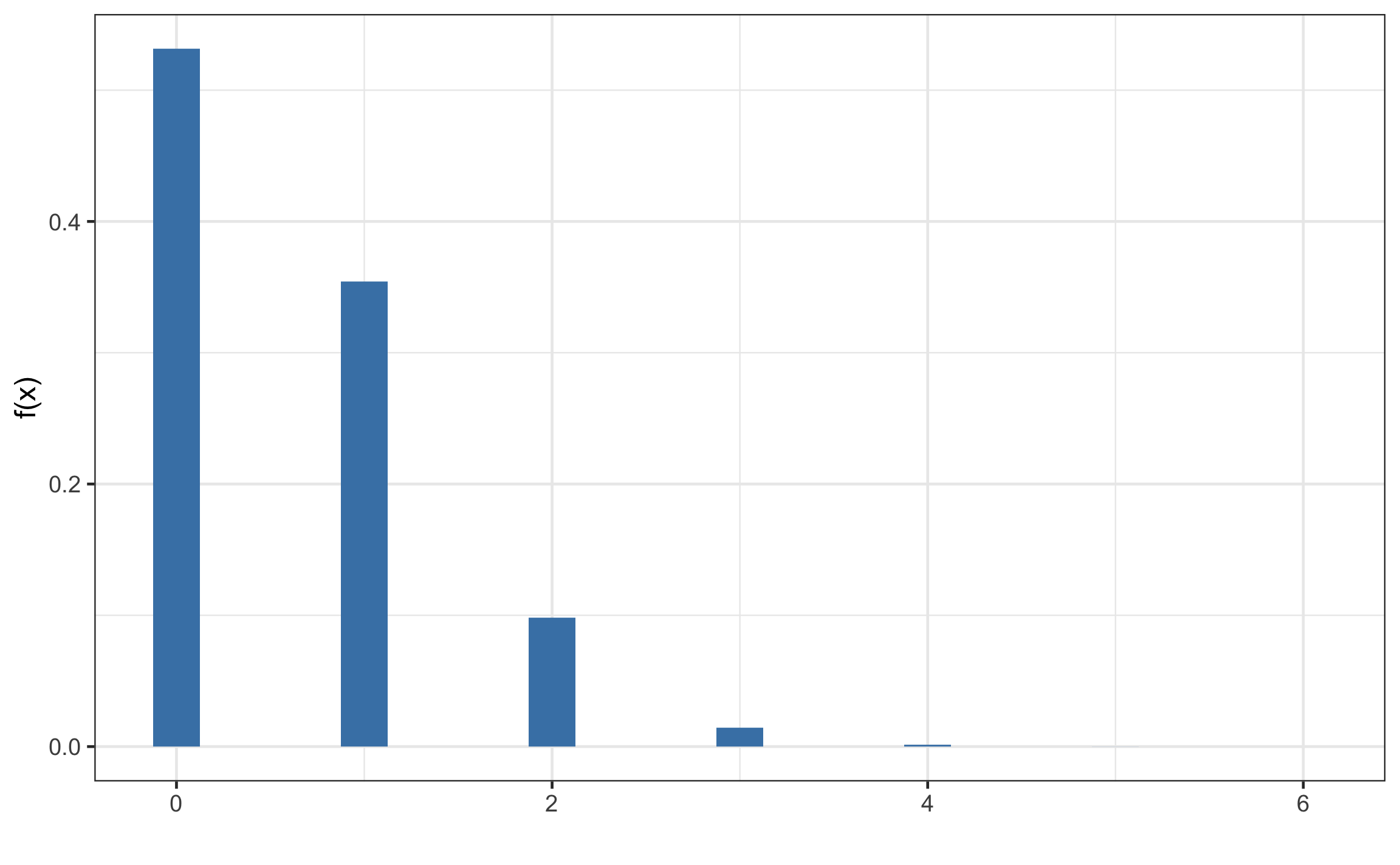
Figura 12.1: Función de probabilidad binomial para los datos del ejemplo.
Esta distribución se puede caracterizar por medio de los parámetros \(\mu=pq\) y \(\sigma=\sqrt{npq}\), donde éstos corresponden con la media y desviación estándar de una aproximación a la distribución normal (Triola, 2004; Walpole et al., 2012), la cual se va a introducir más adelante. El efecto de estos parámetros se puede visualizar en la Figura 12.2, donde se grafica la distribución de probabilidad y se observa como se puede aproximar a la distribución normal definida por dichos parámetros.
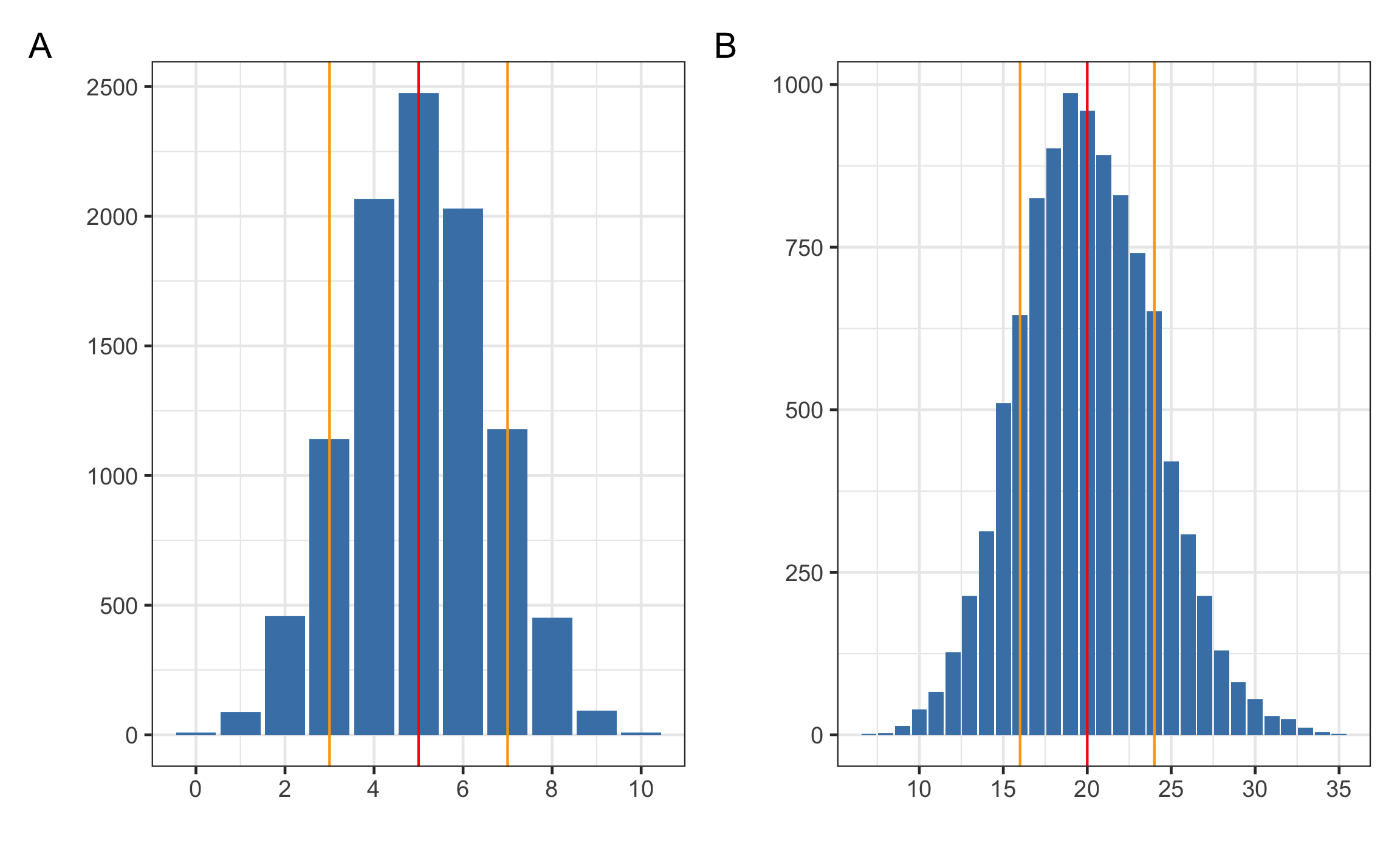
Figura 12.2: Aproximación de la distribución binomial a la normal por medio de los parámetros de la media y desviación estándar, mostrando la ubicación de la media y una desviación estándar por debajo y encima de la misma.
El caso de la Figura 12.2 A corresponde con una variable distribuida binomialmente con 10 intentos y una probabilidad de éxito de 0.5 (\(Bin(10,0.5)\)), dando como resultado los siguientes parámetros:
\[\begin{equation} \mu = np = 10 \cdot 0.5 = 5\\ \sigma = \sqrt{npq} = \sqrt{10 \cdot 0.5 \cdot 0.5} = 1.58 \approx 2 \end{equation}\]
El caso de la Figura 12.2 B corresponde con una variable distribuida binomialmente con 100 intentos y una probabilidad de éxito de 0.2 (\(Bin(100,0.2)\)), dando como resultado los siguientes parámetros:
\[\begin{equation} \mu = np = 100 \cdot 0.2 = 20\\ \sigma = \sqrt{npq} = \sqrt{100 \cdot 0.2 \cdot 0.8} = 4 \end{equation}\]
12.3 Distribución de Poisson
Esta distribución aplica para variables discretas, para eventos que se presentan en una región (distancia, área, volumen) o intervalo de tiempo. Estos eventos, aleatorios e independientes, se consideran poco probables en largos intervalos de ocurrencia, y la cantidad puede ser infinita. Ejemplos de eventos que se pueden caracterizar serían: terremotos, erupciones volcánicas, inundaciones, etc. (Trauth, 2015; Triola, 2004; Walpole et al., 2012).
La Ecuación (12.2) muestra cómo se pueden obtener probabilidades para esta distribución, donde se tiene una variable \(X\) distribuida de forma Poisson con \(\lambda\) como único parámetro, que corresponde con un promedio de eventos por unidad de tiempo o espacio (\(t\)), y \(x \ (0,1,2,\cdots)\) representa el número de eventos.
\[\begin{equation} X \sim Poiss(\lambda) = \frac{e^{-\lambda t}(\lambda t)^x}{x!} \tag{12.2} \end{equation}\]
Para demostrar y visualizar esta distribución se presenta el siguiente ejemplo, modificado de Triola (2004). Al analizar los impactos de las bombas V1 en la Segunda Guerra Mundial, el sur de Londres se subdividió en 576 regiones, cada una con un área de 0.25 \(km^2\). En total, 535 bombas estallaron en el área combinada de 576 regiones.
- Si se selecciona una región aleatoriamente, calcule la probabilidad de que fuese blanco de impactos exactamente en dos (\(x=2\)) ocasiones.
- Con base en la probabilidad que se calculó en el inciso a, ¿cuántas de las 576 regiones se espera que reciban impactos exactamente dos veces?
Se tiene que calcular \(\lambda\) el promedio de impactos por región (\(t=1\)), y se pide la probabilidad de \(x=2\) impactos y la probabilidad de 3 o más impactos. Una representación de la función (distribución) de densidad para este caso se muestra en la Figura 12.3. De manera manual se puede resolver de la siguiente manera.
\[\begin{equation} \lambda = \frac{535}{576} = 0.929\\ Poiss(0.292) = \frac{e^{-0.929 * 1}(0.929 * 1)^2}{2!} = 0.17 = 17 \%\\ \text{Número de regiones que pudieran recibir 2 impactos} = 576 * 0.17 = 97.9 \end{equation}\]
En R se puede usar dpois para obtener la probabilidad puntual y ppois para obtener la probabilidad acumulada.
lambda = 535/576
x = 2
dpois(x = x, lambda = lambda) # probabilidad de x = 2## [1] 0.1703929ppois(q = 2, lambda = lambda, lower.tail = F) # probabilidad de x >= 3## [1] 0.06768529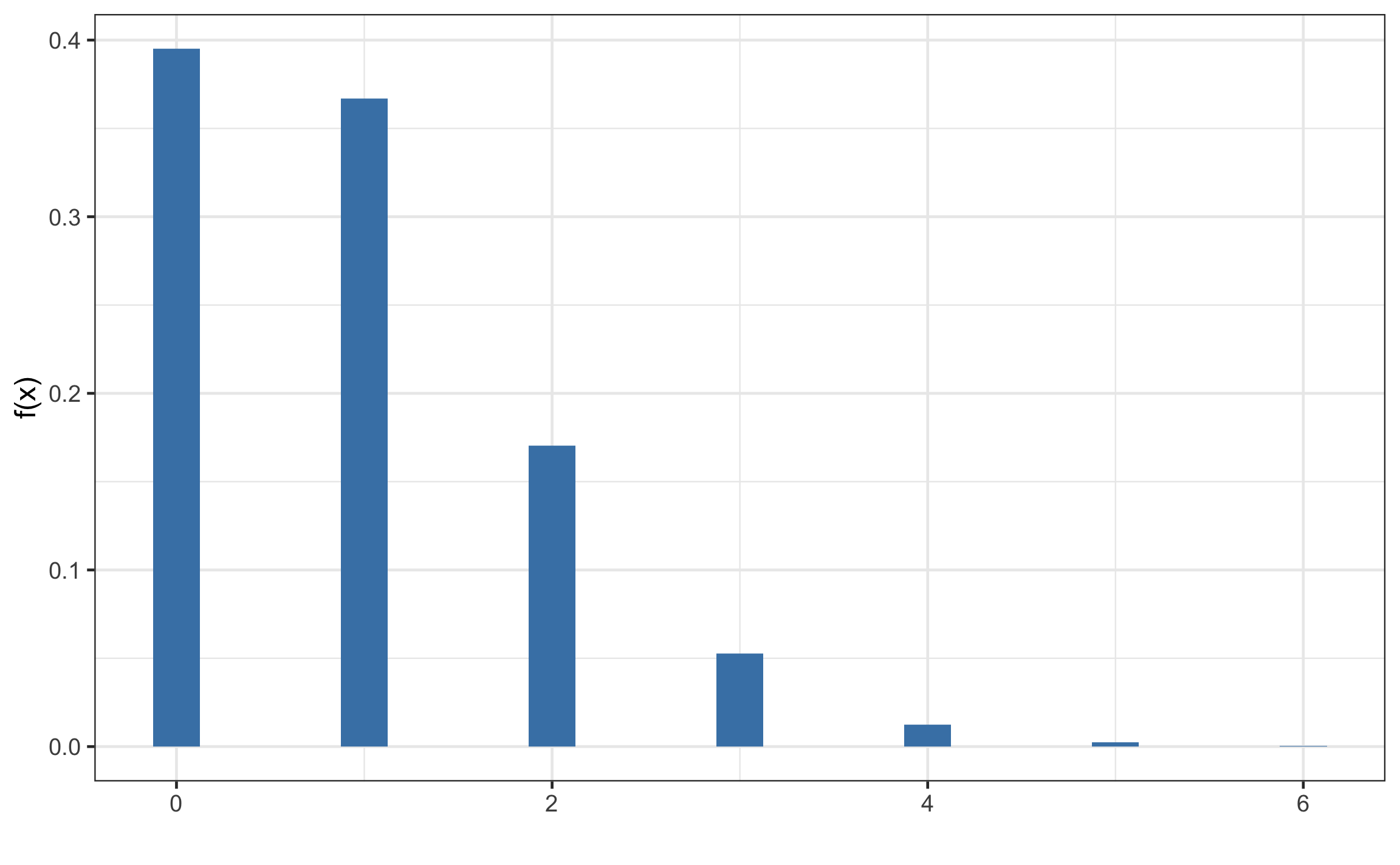
Figura 12.3: Función de probabilidad de Poisson para los datos del ejemplo.
Esta distribución se puede caracterizar por medio de los parámetros \(\mu=\lambda\) y \(\sigma=\sqrt{\lambda}\), donde éstos corresponden con la media y desviación estándar de una aproximación a la distribución normal (Triola, 2004; Walpole et al., 2012). El efecto de estos parámetros se puede visualizar en la Figura 12.4, donde se grafica la distribución de probabilidad y se observa como se puede aproximar a la distribución normal definida por dichos parámetros.
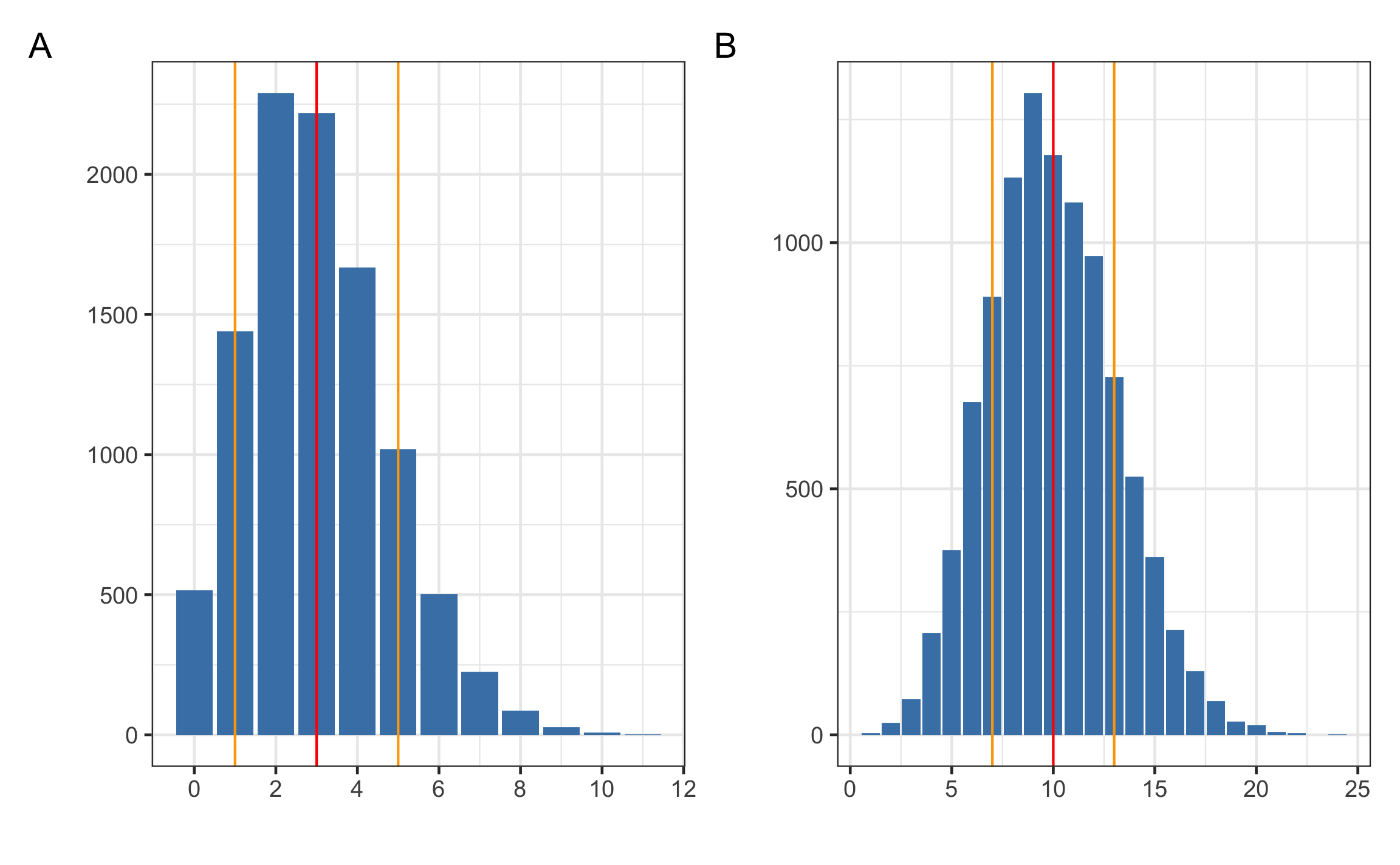
Figura 12.4: Aproximación de la distribución de Poisson a la normal por medio de los parámetros de la media y desviación estándar, mostrando la ubicación de la media y una desviación estándar por debajo y encima de la misma.
El caso de la Figura 12.4 A corresponde con una variable distribuida como Poisson con \(\lambda=3\) (\(Poiss(3)\)), dando como resultado los siguientes parámetros:
\[\begin{equation} \mu = \lambda = 3\\ \sigma = \sqrt{\lambda} = \sqrt{3} = 1.73 \approx 2 \end{equation}\]
El caso de la Figura 12.4 B corresponde con una variable distribuida como Poisson con \(\lambda=10\) (\(Poiss(10)\)), dando como resultado los siguientes parámetros:
\[\begin{equation} \mu = \lambda = 10\\ \sigma = \sqrt{\lambda} = \sqrt{10} = 3.16 \approx 3 \end{equation}\]
12.4 Distribución Normal o Gaussiana
Esta distribución es utilizada para variables continuas, y es la más utilizada en estadística porque “describe de manera aproximada muchos fenómenos que ocurren en la naturaleza, la industria y la investigación” (Walpole et al., 2012). Tiene una forma de campana donde los valores más frecuentes o probables se encuentran en la parte central y los valores menos frecuentes o probables se encuentran en las colas (Figura 12.5)
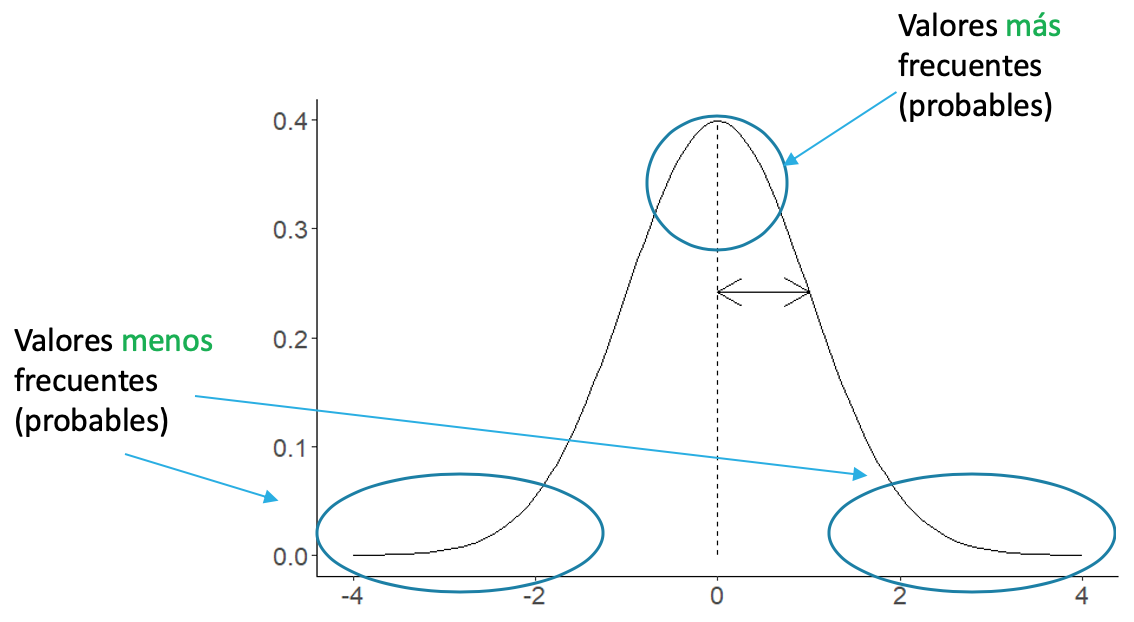
Figura 12.5: Forma de la distribución normal mostrando donde se presentan los valores más y menos frecuentes.
Esta distribución se puede describir por medio de los parámetros de la media (\(\mu\)) y desviación estándar (\(\sigma\)), donde la media representa el valor más probable (Trauth, 2015). Para indicar que una variable se distribuye normalmente se usa la siguiente sintaxis:
\[\begin{equation} X \sim N(\mu,\sigma) \tag{12.3} \end{equation}\]
Las características principales de esta distribución son (Walpole et al., 2012):
- Simétrica alrededor de \(\mu\)
- Centrada y con valor máximo en \(\mu\)
- Puntos de inflexión en \(x = \mu \pm \sigma\)
- El área bajo la curva es 1
La Figura 12.6 demuestra cómo afectan la media y desviación estándar la forma de la curva comparando dos curvas.
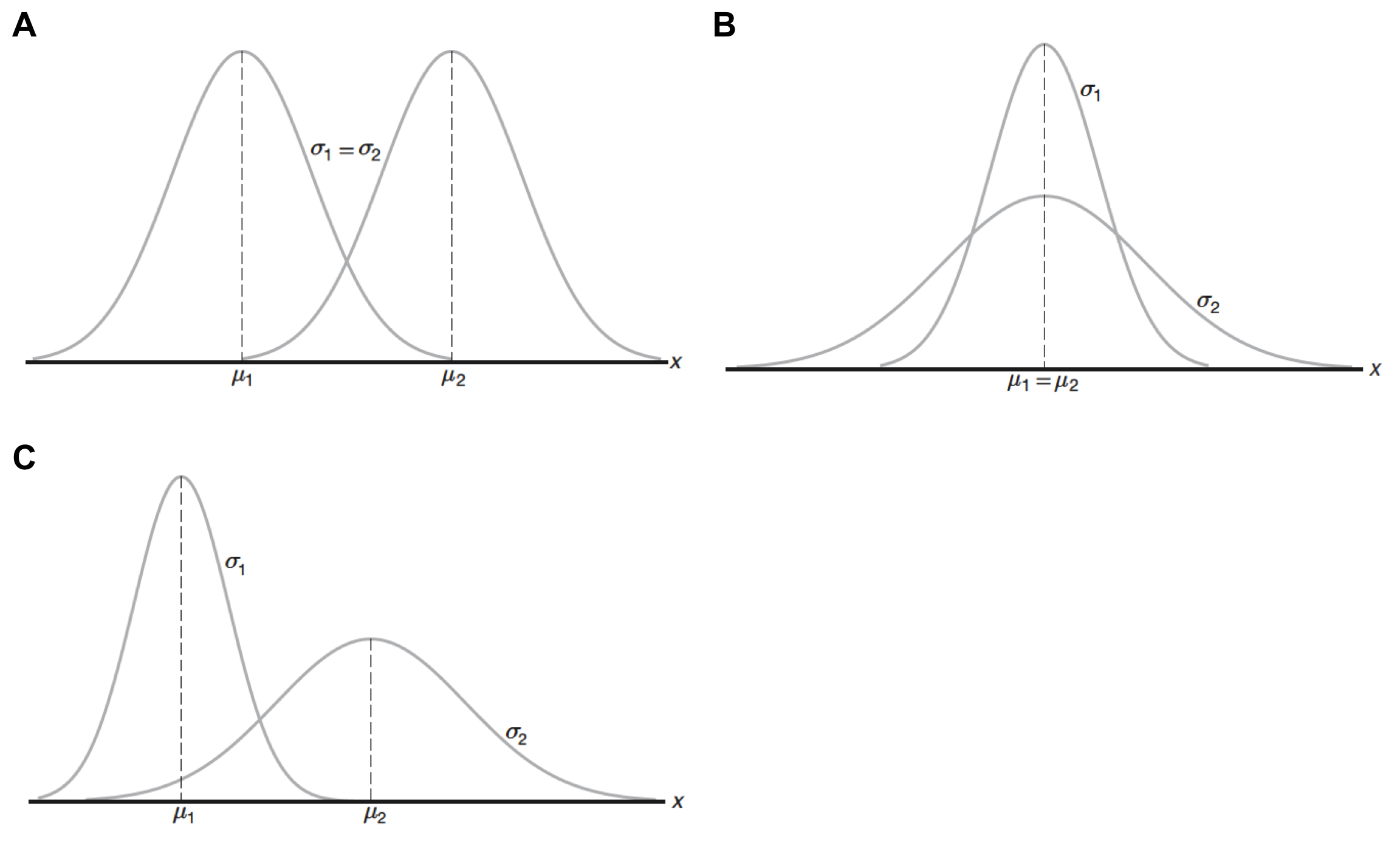
Figura 12.6: Comparación entre curvas normales con diferentes parámetros. A con diferente media (\(\mu_1 < \mu_2\)) pero misma desviación estándar (\(\sigma_1 = \sigma_2\)). B con misma media (\(\mu_1 = \mu_2\)) pero diferente desviación estándar (\(\sigma_1 < \sigma_2\)). C con diferente media (\(\mu_1 < \mu_2\)) y diferente desviación estándar (\(\sigma_1 < \sigma_2\)). Tomado de (Walpole et al., 2012).
12.4.1 Distribución Normal Estándar (Z)
Un caso especial de la distribución normal es la distribución normal estándar. Ésta se caracteriza por tener una media de o y desviación estándar de 1 (Triola, 2004; Walpole et al., 2012).
Para transformar (estandarizar) una variable se usa la Ecuación (12.4) y se describe que esta nueva variable estandarizada está distribuida normalmente con media 0 y desviación estándar 1.
\[\begin{equation} Z = \frac{x - \mu}{\sigma}\\ Z \sim N(0,1) \tag{12.4} \end{equation}\]
El área bajo la curva original y la curva estandarizada es la misma (Figura 12.7), entonces las probabilidades son las mismas, además es útil para comparar distribuciones aún cuando tienen diferentes escalas y/o unidades (Walpole et al., 2012).
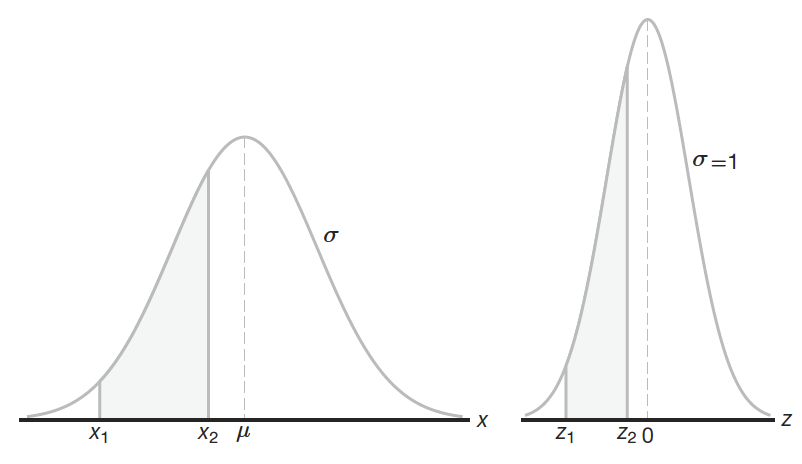
Figura 12.7: El área bajo la curva original es la misma que bajo la curva estandarizada, por ende las probabilidades son las mismas (Walpole et al., 2012).
Se va a demostrar cómo utilizar la curva normal estándar (\(Z\)) para obtener probabilidades por medio de ejemplos tomados de Walpole et al. (2012). El procedimiento manual general es calcular \(Z\) y buscar el área a la izquierda para este valor (tablas de distribuciones en Walpole et al. (2012)), y dependiendo de lo que se pida se realiza algún cálculo adicional.
Dada una variable aleatoria X que tiene una distribución normal con \(\mu=50\) y \(\sigma=10\), calcule la probabilidad de que X tome un valor entre 45 y 62. La idea es obtener al área a la izquierda del valor mayor y restarle el área a la izquierda del valor menor, obteniendo así la intersección (Figura 12.8).
\[\begin{equation} X \sim N(50,10)\\ z_1 = \frac{45 - 50}{10} = -0.5\\ z_2 = \frac{62 - 50}{10} = 1.2\\ P(45 < X < 62) = P(-0.5 < Z < 1.2) = P(Z < 1.2) - P(Z < -0.5)\\ P(Z < 1.2) - P(Z < -0.5) = 0.8849 - 0.3085 = 0.5764 = 57.6 \% \end{equation}\]
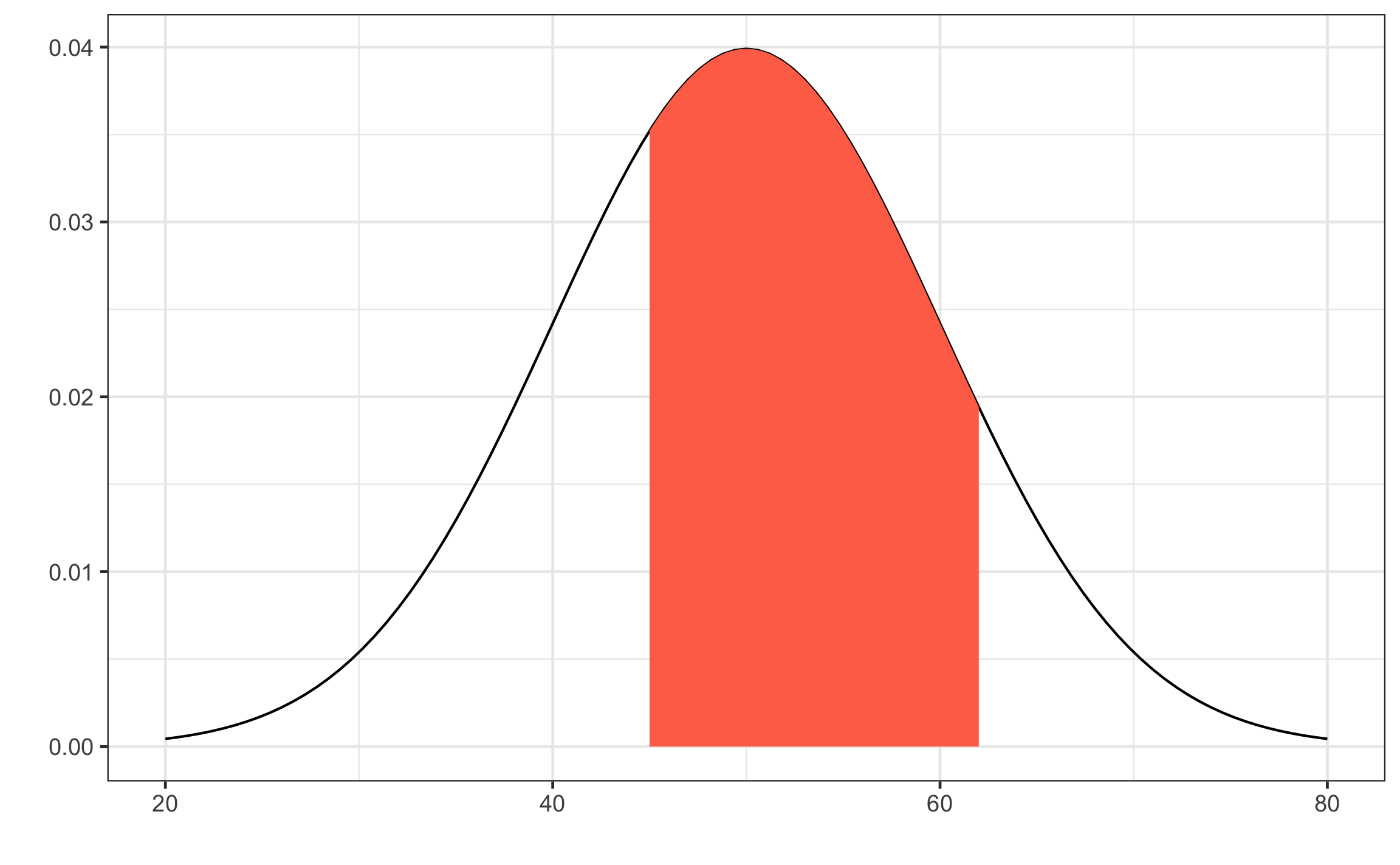
Figura 12.8: Curva normal para el ejemplo mostrando el área entre los valores de 45 y 62.
En R se realiza como se muestra, usando pnorm, donde esta función va a calcular, por defecto, el área a la izquierda para \(x=q\) con una media \(\mu\) y desviación estándar \(\sigma\). La función pnorm y el resto de funciones relacionadas con la distribución normal tienen por defecto una media de 0 y desviación estándar de 1, correspondiendo con la distribución normal estándar, por lo que se pueden usar valores de \(z\) directamente y obtener los mismos resultados.
mu = 50
sigma = 10
x1 = 45
x2 = 62
z1 = (x1 - mu) / sigma
z2 = (x2 - mu) / sigma
pnorm(q = x2,mean = mu,sd = sigma) - pnorm(q = x1,mean = mu,sd = sigma)## [1] 0.5763928pnorm(q = z2) - pnorm(q = z1)## [1] 0.5763928Dado que X tiene una distribución normal con \(\mu=300\) y \(\sigma=50\), calcule la probabilidad de que X tome un valor mayor que 362. Aquí la idea es obtener el área a la derecha de 362 (Figura 12.9), por lo que hay que encontrar el área la izquierda y restárcela a 1.
\[\begin{equation} X \sim N(300,50)\\ z = \frac{362 - 300}{50} = 1.24\\ P(X > 362) = P(Z > 1.24) = 1 - P(Z > 1.24)\\ 1 - P(Z > 1.24) = 1 - 0.8925 = 0.1075 = 10.7 \% \end{equation}\]
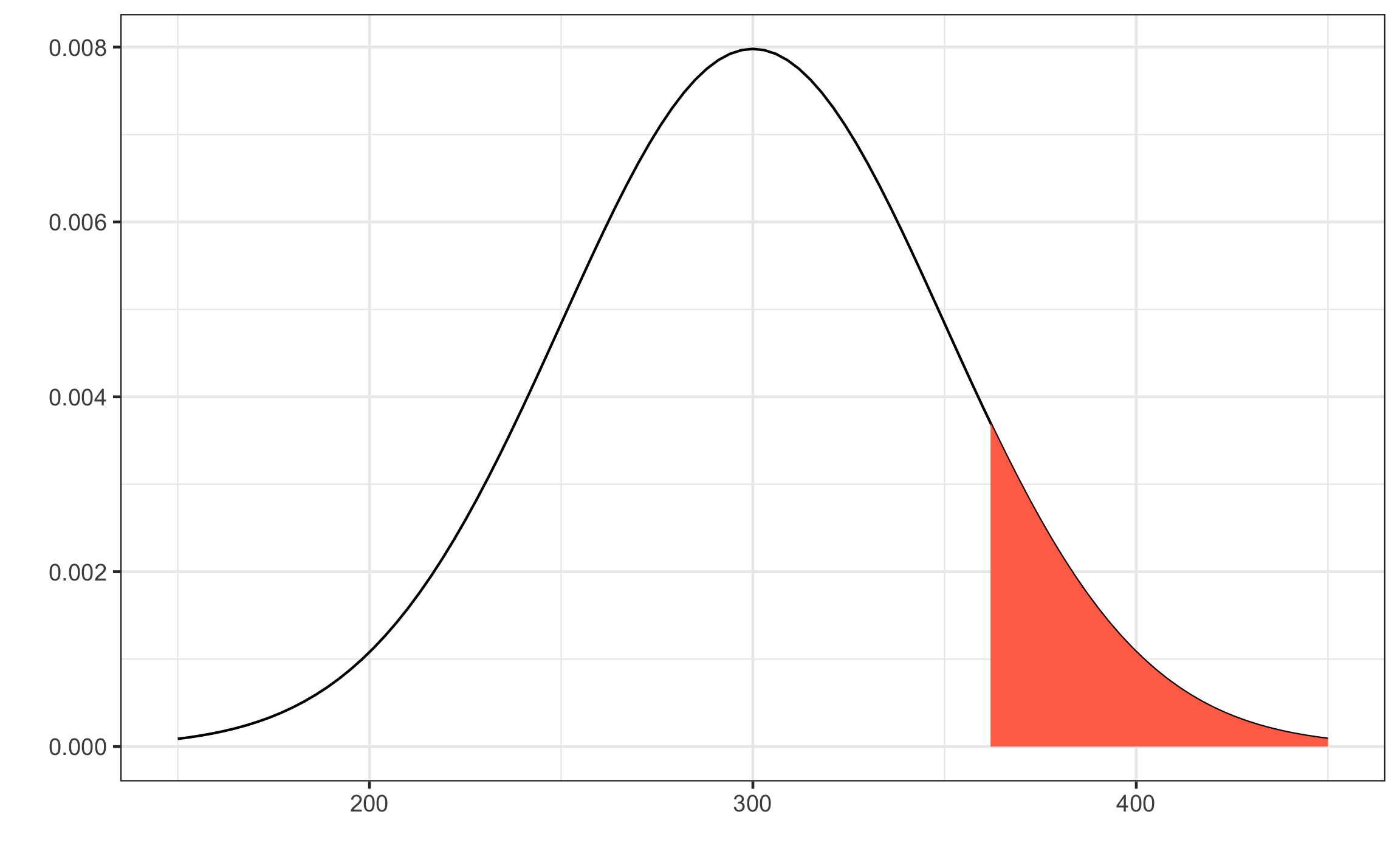
Figura 12.9: Curva normal para el ejemplo mostrando el área a la derecha de 362.
En R se realiza como se muestra, usando pnorm, donde esta función va a calcular, por defecto, el área a la izquierda para \(x=q\) con una media \(\mu\) y desviación estándar \(\sigma\). Para calcular el área a la derecha se puede restar el resultado a 1 o se puede usar el argumento lower.tail = F para obtener directamente el área a la derecha.
mu = 300
sigma = 50
x = 362
z = (x - mu) / sigma
pnorm(q = x,mean = mu,sd = sigma,lower.tail = F)## [1] 0.10748771 - pnorm(q = z)## [1] 0.1074877Así como se puede calcular la probabilidad para un \(x\) se puede a partir de una probabilidad dada encontrar el \(x\) que corresponde con dicha probabilidad. Se muestra un ejemplo a continuación.
Dada una distribución normal con \(\mu = 40\) y \(\sigma = 6\), calcule el valor de \(x\) que tiene: 45% del área a la izquierda, y 14% del área a la derecha (o sea 86% área a la izquierda), ver Figura 12.10. Para ésto se despeja \(x\) de la Ecuación (12.4) y se tiene que encontrar el valor de \(z\) que corresponde con la probabilidad dada.
\[\begin{equation} p = 0.45, \text{resultando en un } z = -0.13\\ x = \sigma * z + \mu = 6 * -0.13 + 40 = 39.24\\ p = 0.86, \text{resultando en un } z = 1.08\\ x = \sigma * z + \mu = 6 * 1.08 + 40 = 46.48 \end{equation}\]
En R se usa la función qnorm para encontrar el valor de la variable para una probabilidad dada.
qnorm(.45,40,6)## [1] 39.24603qnorm(.14,40,6,lower.tail = F)## [1] 46.48192qnorm(.86,40,6)## [1] 46.48192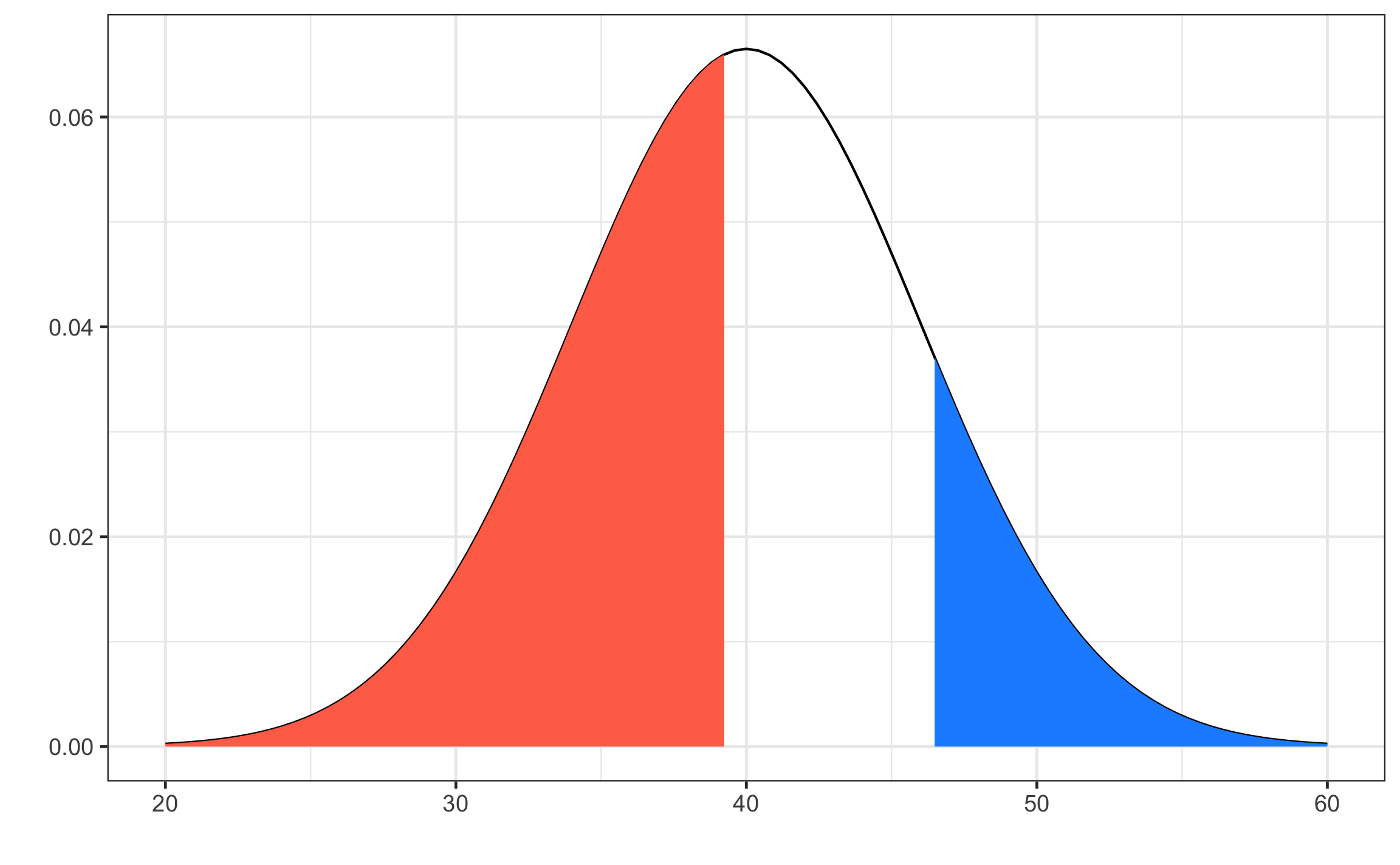
Figura 12.10: Curva normal para el ejemplo mostrando el valor para un área a la izquierda de 45% (coral) y el valor para un área a la derecha de 14% (celeste).
12.5 Distribuciones de probabilidad en R
R tiene funciones para las distribuciones más usadas (Tabla 12.1). Existen 4 funciones generales para todas las distribuciones, donde empiezan con la misma letra y después le sigue el nombre de la distribución:
d*: Las funciones que empiezan condcalculan la probabilidad puntual. Éstas aplican más para distribuciones discretas (binomial, poisson).p*: Las funciones que empiezan conpcalculan la probabilidad acumulada inferior (por defecto) o superior. Éstas aplican para todas pero especialmente para las distribuciones continuas (normal, \(Z\), \(t\), \(\chi^2\), \(F\)).q*: Las funciones que empiezan conqcalculan el valor de la variable o estadístico (cuantil) que corresponde con cierta probabilidad.r*: Las funciones que empiezan conrgeneran datos aleatorio (random) para la distribución deseada y con los parámetros deseados.
| Distribucion | Puntual | Acumulada | Cuantil | Aleatorios |
|---|---|---|---|---|
| Binomial | dbinom | pbinom | qbinom | rbinom |
| Poisson | dpois | ppois | qpois | rpois |
| Normal | dnorm | pnorm | qnorm | rnorm |
| t | dt | pt | qt | rt |
| chi2 | dchisq | pchisq | qchisq | rchisq |
| F | df | pf | qf | rf |
Referencias
Trauth, M. (2015). MATLAB® Recipes for Earth Sciences (4.ª ed.). Springer-Verlag Berlin Heidelberg.
Triola, M. F. (2004). Probabilidad y Estadística (9.ª ed.). Pearson Educación.
Walpole, R. E., Myers, R. H., & Myers, S. L. (2012). Probabilidad y Estadística Para Ingeniería y Ciencias. Pearson.